A Special-Purpose Processor
for Gene Sequence Analysis
(barry.fagin@dartmouth.edu)
J. GIll Watt**
Thayer School of Engineering
Robert Gross
(bob.gross@dartmouth.edu)
Department of Biology
Dartmouth College
Hanover, NH 03755
KEYWORDS: dynamic programming,
sequence comparison, special purpose computer.
*To whom reprint requests should be sent
**Current address: Digital Equipment Corporation,
Hudson MA.
ABSTRACT
Advances in computational biology have occurred
primarily in the areas of software and algorithm development; new designs of
hardware to support biological computing are extremely scarce. This is due, we
believe, to the presence of a non-trivial knowledge gap between molecular
biologists and computer designers. The
existence of this gap is unfortunate, as it has long been known that for
certain problems, special-purpose computers can achieve significant
cost/performance gains over general purpose machines.
We describe one such computer here: a custom
accelerator for gene sequence analysis. The accelerator implements a version of
the Needleman-Wunsch algorithm for nucleotide sequence alignment. Sequence lengths are constrained only by
available memory; the product of sequence lengths in the current implementation
can be up to 222. The
machine is implemented as two NuBus boards connected to a Mac II f/x, using a
mixture of TTL and FPGA technology
clocked at 10 MHz. The boards are
completely functional, and yield a 15-fold performance improvement over an
unassisted host.
Introduction
Efforts to use novel architectures for
computational biology are relatively scarce. One of the first attempts was made
by Collins and Coulson (1984), who suggest using a special-purpose Single
Instruction Multiple Data machine for sequence processing. Mukherjee (1989)
discusses efficient hardware algorithms for finding the longest common
subsequence of two strings, although no performance results are reported. Many
supercomputers have received careful attention from researchers, including the
Hitachi S810-20 (Goto and Tagashira, 1986), and the iPSC/1 and the CM-1 (Core
et. al., 1989). Lopresti (1989) has discussed the performance of the Multiflow
Trace, Convex C1, Cray-2, and CM-2 on gene sequence comparison problems.
One of the first successful efforts in the area of special purpose processing
was the Splash highly parallel programmable logic array, developed by Lopresti
and colleagues at the Supercomputing Research Center (see Gokhale 1991). This
machine evolved out of the Princeton Nucleic Acid Comparator, or P-NAC,
developed by Lopresti and Lipton (1987). Both of these machines use a highly
parallel architecture to calculate multiple similarity values in parallel. Like
the Gene Sequence Processor, Splash makes extensive use of field programmable
gate arrays to permit rapid prototyping and flexible implementation. Both
Splash and P-NAC were prototyped successfully. Neither machine, however, is alignment-preserving, That is, neither
machine can produce the alignments corresponding to the similarity scores they
generate (although Splash can in theory be modified to do so, as described by
Hoang [1991]).
More recently, we have identified three
projects concerned with special purpose hardware for sequence comparison: the
Biological Information Signal Processor (Chow 1991), the BioSCAN system (White
1991), and the B-SYS programmable systolic array (Hughey 1991). Both the BISP and BioSCAN systems are full
custom VLSI implementations of systolic arrays: BISP uses a custom chip for
dynamic programming calculations, while BioSCAN implements linear similarity
algorithms using lookup tables stored in an on-chip RAM. B-SYS also uses full custom ASICs, but is a
general purpose programmable systolic array, and hence considerably more
flexible in the algorithms it can support.
The principal difference between the
GSP and these devices is its employment of user-obtainable, off-the-shelf
parts. Our goal was to employ
semi-custom ASICs in a special purpose processor to produce a machine that
could be reproduced and upgraded without the expense of a full custom approach. The GSP also preserves alignments and
calculates similarity scores. We believe
both these features are essential components of a biological processor:
similarity scores are necessary to rank results from library searches, while
alignments assist in visualizing homologous regions and constructing
evolutionary relationships between sequences.
System and Methods
The Gene Sequence Processor was
designed at the Thayer Rapid Prototyping Facility (RPF), a laboratory for the
rapid design and construction of digital systems. The RPF has been involved in
several successful experiments in rapid digital system design. In addition to
the Gene Sequence Processor, other projects include a completely functional
32-bit microprocessor, a Fast Hartley Transform engine, and a real-time data
processor for rocket telemetry. For information on these and other projects,
the reader is referred to (Erickson and Fagin 1992), (Fagin 1991) and (Fagin and Chintrakulchai
1992).
The GSP itself consists of two
11.7" x 4" 2-layer printed
circuit boards, consisting of the following components:
5 Actel Field Programmable Gate Arrays
3 TI NuBus chips
8 1Mb DRAM SIMMs
4 AMD 22V10 PALs
23 miscellaneous TTL IC's
The total cost for these parts is
approximately $750: $400 for the DRAM chips, $250 for the FPGA's, and $100 for
the remaining IC's. Board fabrication
costs are relatively modest, due to the use of an in-house printed circuit
board prototyping system. We estimate
these at around $100.
The GSP board is clocked at 10 MHz, and
requires 6 clock ticks = 600 ns to calculate a dynamic programming array entry.
Algorithm
The algorithm implemented by our
processor is the well-known dynamic programming algorithm for determining the
similarity of two strings (see for example Sellers, 1974 and Kruskal,
1983). For readers unfamiliar with this
technique, we provide an overview of it here.
The Gene Sequence Processor computes
the similarity between two sequences A and B by computing an edit distance: the minimum number of
insertions, deletions, and changes needed to transform sequence A into sequence
B. Our system permits insertions, deletions, and changes to each have their own
associated cost; thus the GSP calculates the least costly sequence of
operations that transforms sequence A
into sequence B.
Consider the minimum cost sequence of
operations needed to transform a sequence A of length m into a sequence B of
length n. Let A’ be the sequence A minus its last character, similarly for
B’. A can be transformed into B in one
of the following ways:
1)
Delete the last character of A and transform A’ into B.
2)
Transform A into B’ and add the last character of B.
3)
Delete the last character of A, transform A’ into B’, and add the last
character of B.
At least one of these methods will
yield a transformation of A to B of minimum cost. But then each of the sequences of operations
in the first part of the definitions above can be defined similarly, by letting
A’’ and B’’ denote the sequences A’ and B’ minus their last characters and
reapplying the above definitions. The process can be repeated until null
sequences are reached, for which the associated costs are zero.
We may mathematically define this process in the following
way. Let A be a sequence of length m, B a sequence of length n,
and let [i] denote the ith
character of a sequence. Let the minimum
distance between A and B be the
total cost of the least costly series of insertions, deletions, and
substitutions needed to transform A into B. Then D[m,n ], the minimum distance between A and B, is given by:
D[0,0] = 0 (I)
D[i,0] =
D[i-1,0] + del (A[i]) 1 _ i _ m (II)
D[0,j] =
D[0,j-1] + ins (B[j]) 1 _ j _ n (III)
D[i,j] =
minimum{D[i-1,j] + del
(A[i]), D[i,j-1] + ins (B[j]),
D[i-1,j-1] + subs (A[i],B[j])}
1
_ i _ m, 1 _ j _ n (IV)
where
the functions ins, del, and subs denote the cost of insertion, deletion,
and substitution respectively. Lines II, III, and IV correspond to definitions
1, 2, and 3 above.
Let us number the matrix D with
increasing subscripts from top to bottom and left to right. The task of
computing the minimum distance between two sequences of lengths m and
n requires
the calculation of each entry in this array, in which the value of a cell is
dependent on the values of its left, upper left, and upper neighbors. An example matrix and cost functions for m = 3, n = 5 is shown in Figure 1. The minimum distance to completely
transform sequence A into sequence B, 8, appears in the lower right hand corner
of the array; the cost functions used are shown at the top of the picture.
Notice that if information is kept with
each cell recording which sum in (IV) is the minimum, then the entire sequence
of operations corresponding to the minimum distance can be reconstructed. This
gives an optimal alignment, a way of
positioning the sequences relative to one another so that similarities can be
easily seen. The example of Figure 1, modified with special information to
reconstruct the alignment, is shown in Figure 2.
The special information is kept in the
form of back pointers, numbers that
indicate which entry in the array corresponds to the smallest neighbor. In
general, all cells will have back pointers; for clarity only those pointers in
the optimal alignment are shown. Notice that more than one optimal alignment
may exist, corresponding to multiple paths of back pointers from the lower
right corner to the upper left.
The processor we have constructed
implements the calculations described by (I) through (IV), using back pointers
to save the final alignment and return it to the host. We note that although
(I) through (IV) are used to calculate global alignments, our processor can
also be used to implement local alignment calculation. The initial sequences A
and B are transferred from the host, along with the values for the ins, del,
and subs functions. The dynamic programming
calculation then begins, using special hardware to accelerate the comparison
operation in (IV).
In addition to the operations specified
in (I)-(IV), the GSP permits the incorporation of initial costs for gaps
between sequences. Thus models with
linear gap costs, which incorporate both the number of nucleotides in the gap
and some initial constant penalty can be accommodated by the GSP.
We note that the global alignment
calculated in Figures 1 and 2 may not in and of itself be biologically
significant. Global alignments involving complete sequence conversion which may
contain multiple insertions or deletions at the ends of a sequence, for
example, clearly contain superfluous information. Significant alignment
information, however, is contained in the dynamic programming matrix computed
by the GSP, which can then be traversed by software to identify alignments of
importance. For more information on alignment extraction from a dynamic
programming matrix, the reader is referred to Gribskov and Devereux (1991).
Implementation
A block diagram of the Gene Sequence
Processor is shown in Figure 3. The GSP consists of five basic subsystems:
alignment memory, sequence memory, a counter/comparator, the interface with the
host computer, and the Gene Arithmetic Logic Unit. It implements a dynamic
programming algorithm to compute the minimum cost of insertions, deletions, and
substitutions necessary to transform one nucleotide sequence into another,
based on a set of cost functions supplied by the user. The total cost of this
sequence of operations is the edit distance between A and B.
The GSP contains 8 megabytes of
alignment memory, used to hold the dynamic programming array in Figure 1. This
memory is organized as 222 16-bit words of
dynamic random access memory, or DRAM, limiting the product of the lengths of
the sequences to be compared to 222. The
format of a DRAM word is shown in Figure 4. Each byte is broken into 6 bits of
data and a 2 bit field for the back pointer.
Back pointer information was made
identical in each byte to simplify the design of the processor, leaving 12 bits
of data in each array entry. Thus, the maximum edit distance the GSP can
compute is 212 = 4096. Currently, cost function values are
constrained to be integers. This has not proven to be a limiting factor in our
experiments.
The sequences to be compared, cost
function values, and sequence lengths are downloaded into sequence memory,
organized as 4096 bytes of static random access memory, or SRAM. The
counter/comparator is used to generate the necessary addresses for the dynamic
programming calculation, and to halt the computation when the last entry in the
dynamic programming array has been calculated. The processor interface is
responsible for all interaction with the host computer.
A block diagram of the Gene Arithmetic
Logic Unit, or ALU, is shown in Figure 5. The relevant cost coefficients and
array values are added in parallel, and sent to a customized 3-way comparator
that determines the minimum value. This value is then written back into the
dynamic programming array; the letters “DP” and subscripts in Figure 5 refer to
the relevant array entries.
The nucleotides as compared by the
Gene ALU are encoded in the 4-bit representation shown in Table I. Each bit in the 4-bit representation
corresponds to a specific nucleotide. This arrangement allows for the use of
the standard IUPAC nucleotide code as shown in the table. A match occurs if any bits in a given
position are '1' for both nucleotides.
For example, the Gene ALU will detect a match between "C" and "Y",
because both have a '1' in their second bit position.
Discussion
The
performance of the GSP is shown in Figure 6, in which the sequence comparison
time of the GSP is compared with that of the unaided host. Host execution times
were measured running a C implementation of the dynamic programming algorithm.
We deliberately made this program as fast as possible, to avoid biasing the
results in favor of the GSP. Execution time is shown on the vertical axis,
plotted against the number of nucleotides. For these measurements, both
sequences are assumed to be of the same length.
Figure 6 also shows the execution time
of the same C code on an IBM RS6000 workstation and a Sun Sparc. The results are real time measurements,
running under UNIX with a single user.
Both object files were produced with the same compiler. We see that the results for both workstations
are comparable to the f/x.
Figure 6 shows an average performance
improvement of about 15-fold. Note that despite the appearance of the graph,
GSP performance scales quadratically, due to the quadratic nature of the
algorithm. The resulting execution times
are very close to 600(n+1)2/109, since the processor runs at 10Mhz and requires 6
clock cycles to calculate a dynamic programming array entry.
For a performance comparison of the GSP
with other machines, and a more detailed discussion of the architecture and
technology, the reader is referred to Fagin and Watt (1992).
Biologists wishing to use the GSP need
only be familiar with the look and feel of the Macintosh; no other special
skills are necessary. The software interface to the GSP uses the standard
Macintosh tools, and is quite flexible. One can use the GSP and existing
software to view color comparisons of sequences, examine long alignments using
scroll boxes, and compute alternative alignments with different cost functions.
When constructing a special-purpose processor, the danger of the “architect's
trap” is especially strong: one must be careful to not put so many features
into hardware that the flexibility and cost-effectiveness of the system are
compromised. By incorporating a considerable amount of system flexibility in
the GSP user interface, we believe we have avoided this problem.
Examples of GSP/user interaction are
shown in Figures 7 and 8. When the processor is connected to the host and
powered on, the user double-clicks on a standard Macintosh software icon to
obtain the dialog box in Figure 7. The user then specifies the names of two
files on her disk, containing the two sequences to be compared. She can then
specify insertion, deletion, and substitution costs, as well as insertion and
deletion gap penalties; the values shown in the figures are merely defaults,
and can be changed with the mouse and keyboard.
Other features include advanced debugging output and a post-processing
analysis of the complete dynamic programming array. We note that all of these tasks are
accomplished using the standard Macintosh user interface and mouse.
Once the parameters of the run have
been entered, the user clicks “Done”. Some timing information will be printed,
followed by the display of the optimal alignment and corresponding edit
distance as shown in Figure 8. Users can view large alignments in their
entirety, scrolling to the left or right one character at a time (small arrows)
or one window at a time (large arrows).
Conclusions and Future Work
The initial goal of this project was to construct
an attached processor for gene sequence analysis that would offer an order of
magnitude improvement in performance over personal computers at a minimal cost.
Our efforts were successful: the Gene Sequence Processor has met or exceeded
design specifications.
Nonetheless, much can be done to
improve it. The main performance
limitations on the GSP are the 10MHz clock and the DRAM interface. The present design requires one read and write
per cell, each of which requires three clock cycles to implement. The 10MHz clock is taken directly from the
NuBus; employing a design with a separate clock could in principle reduce the
cell calculation time from 600ns to 320ns.
The critical path through the system would then be through the FPGA's,
which could be reduced to about 225ns through the use of a carry-lookahead
scheme for the Gene ALU. Using a static
RAM cache and DRAM page mode access could reduce memory access time even
further, at the cost of increased system complexity.
Sequence lengths can be extended
through the addition of more DRAM; up to 32Mb can be accommodated with minimal
modifications to the existing design.
Currently, only nucleotide sequences can be accommodated; future versions
will support amino acid comparisons. We
believe this can be accomplished by simply reprogramming the FPGA's, and are
currently investigating this possibility.
Furthermore, the basic dynamic
programming algorithm described here, while optimal, is known to be
unnecessarily slow. More heuristically-oriented algorithms like those used in
the FASTA (Wilbur and Lipman, 1983) and BLAST (Altschul et. al. 1990) software
packages should be investigated. These algorithms are less regular than
Needleman-Wunsch, and hence may pose more of a challenge to a custom processor.
It is also known that the full
calculation of all cells in the dynamic programming array is inefficient (Ukkonen 1983). By
restricting cell calculations to those with distances less than a
predetermined upper limit, significant performance improvement can be obtained
(Spouge 1991). We believe that this type
of optimization can be accommodated by the GSP with minimal effort, requiring
only modifications to the control logic to permit addresses to be skipped if a
critical distance has been exceeded. We
intend to support this feature in the next GSP prototype.
Finally,
we believe a 15-fold improvement in performance, while acceptable for a
preliminary prototype, is insufficient for a truly effective biological
computer. Special purpose devices generally require two or three orders of
magnitude of effectiveness to warrant their employment over general purpose
devices, due to the natural advantages of products developed in an active
commercial environment and the rapid rate of improvement of general purpose
computing technology.
We hope, therefore, to improve both the
performance and the software capabilities of the machine by at least another
order of magnitude, to produce a truly significant research tool of general
interest to molecular biologists. This will require the use of more aggressive
technology in the machine itself, a more sophisticated user interface, and
deeper study into the specific computational requirements of important
biological problems.
It is our hope that by combining insights from
computer engineering and molecular biology, we may be able to produce machines
better suited to computational biology than those that currently exist. The
ultimate goal of our research is the production of a machine that can reduce
the time of significant tasks of computational biology, such as database
searching and similarity detection, from minutes or hours to seconds. Such computational capability, we believe,
will permit biologists to more rapidly and efficiently evaluate the
implications of nucleotide and protein sequence data, and to generate new
insights into the nature of genomic information. This will become possible when
sequence comparisons can be performed in an interactive mode rather than in a
batch mode. Work on this topic is currently in progress.
Acknowledgements
The authors gratefully acknowledge the assistance
of the Whitaker Foundation, whose generosity made the construction of the GSP
possible. Support for the Rapid Prototyping Facility was provided by a variety
of sources, including Actel, Altera, Xilinx, Sun Microsystems, Viewlogic,
National Semiconductor, and Direct Imaging Incorporated. Additional support was
provided by the Thayer School of Engineering, and the National Science
Foundation, award #CDA-8921062.
References
Altschul,
S.F., Gish, W., Miller, W., Myers, E.W., Lipman, D.J. (1990). Basic Local
Alignment Search Tool. J. Mol. Biol. 215:
403-410.
Chow, E. T. et.
al. (1991) A Systolic Array Processor For Biological Information Signal
Processing. Proceedings of the 1991 International Conference on Supercomputing,
1991, pp 216-223.
Collins, J.F.
and Coulson, A.F.W. (1984) Applications of Parallel Processing Algorithms for
DNA Sequence Analysis. Nucleic Acids
Res., 12, 181-192.
Core, N. et.
al. (1989) Supercomputers and Biological Sequence Comparison Algorithms. Computers and Biomedical Research, 22, 497-515.
Erickson,
A. and Fagin, B. (1992) Calculating the
FHT in Hardware, IEEE Transactions
on Signal Processing, June 1992
(in press).
Fagin, B. (1991) Using Antifuse-Based FPGAs in
Performance-Critical Digital Designs, Proceedings
of the 4th Microelectronics System Education Conference and Exposition, San Jose, CA, 225-234.
Fagin, B. and
Watt, G. (1992), FPGA and Rapid
Prototyping Technology Use in a Special Purpose Computer for Molecular
Genetics, Proceedings of the 1992 International Conference on Computer Design,
October 1992 (in press).
Fagin, B. and
Chintrakulchai, P. (1992), Prototyping the DLX Microprocessor, Proceedings of
the 1992 IEEE Workshop on Rapid System Prototyping, Research Triangle Park NC,
(in press).
Gribskov, M.
and Devereux, J. (1991) Sequence Analysis Primer, Stockton Press, Macmillan Inc, New York, NY.
Gokhale, M. et.
al. (1991) Building and Using a Highly Parallel Programmable Logic Array. Computer, 24, 81-89.
Gotoh, O. and
Tagashira, Y. (1986) Sequence Search on a Supercomputer. Nucleic Acids Res., 14,
57-64.
Hoang, D.
(1991) Systolic Array for DNA Sequence Alignment. Brown University Department
of Computer Science Technical Report, December 1991.
Hughey, R.
(1991) Programmable Systolic Arrays. Ph.
D. Dissertation, Department of Computer Science, Brown University, Providence
RI 02912.
Karlin,
S. and Altschul, S. (1990) Methods for Assessing the Statistical Significance
of Molecular Sequence Features by Using General Scoring Schemes. Proc. Natl. Acad. Sci., 87, 2264-2268.
Kruskal, J. B.
(1983) An Overview of Sequence Comparison: Time Warps, String Edits, and Macromolecules.
SIAM Review, 25, 201-237.
Lander, E. S.
et. al. (1991) Computing in Molecular Biology: Mapping and Interpreting
Biological Information. Computer, 24 #11, 6-13.
Lopresti, D. (1987) P-NAC: A Systolic Array
For Comparing Nucleic Acid Sequences. Computer,
20 #7, 98-99.
Lopresti, D.
(1989) Sequence Comparison on Commercial Supercomputers. Supercomputing
Research Center Technical Report SRC-TR-89-010.
Mukherjee, A.
(1989) Hardware Algorithms for Determining Similarity Between Two Strings. IEEE Trans. Comp., 38, 600-603.
Sellers, P. H.
(1974) On the Theory and Computation of Evolutionary Distances.
SIAM J. Appl. Math., 26, 787-793.
Spouge,
J.L. (1991). Fast optimal
alignment. Comput. Appl. Biosci. 7:1-7.
Ukkonen,
E. (1983). On approximate string
matching. Proc. Int. Conf. Found. Comp. Theory, Lecture Notes in Comp. Sci.
158:487-496, Springer-Verlag, Berlin.
White, C. et.
al. (1991). BioSCAN: A VLSI-Based System for Biosequence Analysis,
Proceedings of the 1991 International
Conference on Computer Design, Cambridge MA, 1991, pp 504-509.
Wilbur,
W.J. and Lipman, D.J. (1983) Rapid Similarity Searches of Nucleic Acid and
Protein Data Banks. Proc. Natl. Acad.
Sci., 80, 726-730.
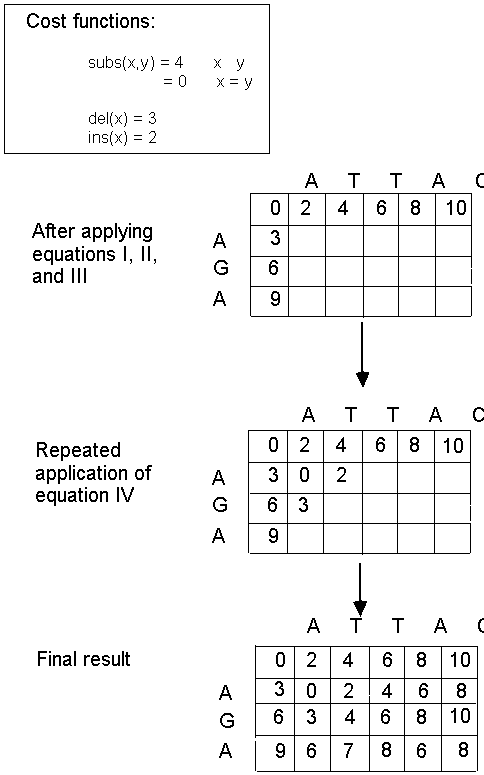
Fig. 1: Sequence Comparison Example
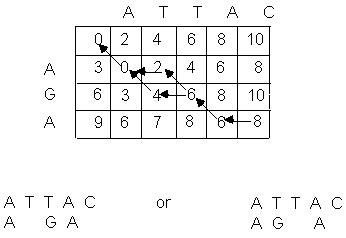
Fig. 2: Sequence Comparison Showing Alignment and
Back Pointers
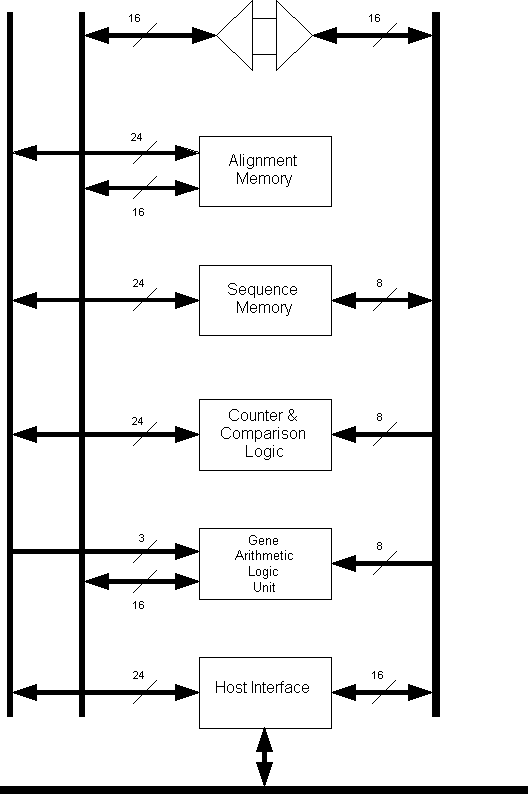
Fig. 3: GSP Block Diagram

Fig. 4: DRAM Word Format
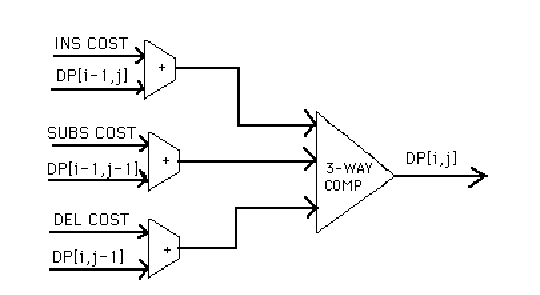
Fig. 5: Gene ALU Block Diagram
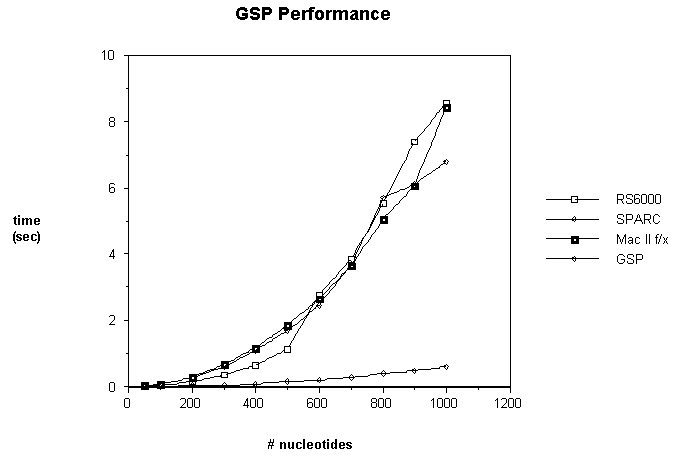
Fig. 6: GSP Performance
Fig. 7: GSP Startup Screen

Fig. 8: Viewing GSP Alignment
TABLES
Nucleotide(s) Letter Binary encoding
Adenosine A 1000
Cytosine C 0100
Guanine G 0010
Thymine T 0001
A or G (puRine) R 1010
C or T (pYrimidine) Y 0101
A or C (aMino, in large groove) M 1100
G or T (Keto, in large groove) K 0011
A or T (Weak) W 1001
A, C, G, or T N 1111
C, G, or T (not A) B 0111
A, G, or T (not C) D 1011
A, C, T (not G) H 1101
A, C, G (not T) V 1110
Table I:
Full Nucleotide Alphabet