Large Integer Multiplication on
Massively Parallel Processors
Barry S. Fagin
Thayer School of Engineering
Dartmouth College
Hanover, NH 03755
barry.fagin@dartmouth.edu
ABSTRACT
We present results of a technique for multiplying
large integers using the Fermat Number Transform. When the Fermat Number Transform was first
proposed, word length constraints limited its effectiveness. Despite the development of multidimensional
techniques to extend the length of the FNT, the relatively small word length of
existing machines made the transform of little more than academic interest. The
emergence of new computer architectures, however, has made the Fermat Number
Transform more attractive. On machines like the Connection Machine, for
example, we may implement the Fermat Number Transform without regard to word
length considerations.
We present a convolution algorithm on a massively
parallel processor, based on the Fermat Number Transform. We present some examples of the tradeoffs
between modulus, interprocessor communication steps, and input size. We then discuss the application of this
algorithm in the multiplication of large integers, and report performance
results on a Connection Machine. Our
results show multiplication times ranging from about 50 milliseconds for 2K-bit
integers to 2600 milliseconds for 8M-bit integers.
The Fermat Number Transform
The
Fermat Number Transform, or FNT, is computationally similar to an FFT, but is
performed in the ring of integers modulo some integer M = 2B +
1. Numbers of this form are called Fermat Numbers. We refer to a ring of integers modulo a
Fermat Number as a Fermat ring. Fermat rings are particularly desirable
for transform operations because multiplication of some binary integer i by 2n
in a Fermat ring is equivalent to a left rotation of i by n bits, followed by
an inversion of the lower n bits.
There
are well known difficulties in using a Fermat ring for computing digital
convolution [1]. For computing
transforms in a ring modulo 2B+1, the maximum possible transform
length is 4B. Since B is the number of
bits necessary to represent integers in the input sequences, it is usually the
word length of the host computer. Most
computers have words no larger than 32 bits, making the use of one dimensional
Fermat Number Transforms impractical for large input sequences.
Agarwal
and Burrus [2] discuss extending the transform length of the FNT through
multidimensional techniques. For a given
sequence length N, a one dimensional convolution with B proportional to N can
be computed using a d-dimensional convolution with B proportional to the dth
root of N. This technique dramatically
extends the range of the FNT to the point where realistic input sizes become
feasible. We use this technique in our
work.
Other
minor difficulties remain. Arithmetic in
a Fermat ring mod 2B+1 on a machine with B-bit words is complicated
by the necessity to represent 2B+1 numbers 0, 1, ... 2B with
B bits. Several techniques have been
proposed to solve this problem. For our
algorithm, we adopt the technique of 1's
reduced notation, first proposed by
Leibowitz [6]. Briefly, a binary number
i such that 1 <= i < 2B is represented by i-1 in 1's reduced
notation. 0 is represented by 2B. This means that 0 can be identified by a 1 in
the B+1st bit, and special procedures invoked to handle this as a special
case. If neither operand is zero,
multiplication of a 1's reduced number by a power of two is equivalent to a
rotation and inversion of bits. Addition
of non-zero operands is similar to binary addition, with the complement of the
carry added to the result. Since
addition and multiplication when one or both of the operands are zero are
trivial operations, the added complexity of this notation is minimal.
We
note that the technological framework of computer design has evolved
considerably since these ideas were first proposed. For new computer architectures like the
Connection Machine, word length considerations are not important. Thus
we may implement the Fermat Number Transform on current multiprocessors
with much less emphasis on word length considerations. Our concern will instead be focused on
reducing the interprocessor communication time and the number of processors, as
we will see shortly.
Digital Convolution Using Multidimensional
FNT's
We
first present an analysis of the tradeoffs involved in using multidimensional
FNT's to compute digital convolution.
Let us assume two input sequences of total bit length N, which we may
partition into digits of some size P >= 1 and convolve using the FNT. For ease of presentation, we assume N, P, and
B are powers of two. Lower case letters
will denote the base 2 logarithm of their upper case equivalents.
We
begin with two sequences of N bits each.
We wish to partition each sequence into P-bit digits, and then compute
their convolution modulo M = 2B+1 using a d-dimensional FNT. For a given N, we wish to understand the
relationships between d, B, and P. In
order for the convolution to be uniquely representable in the Fermat ring mod M
= 2B+1, the maximum value of
a convolution product must be less than or equal to the largest integer in the
ring. Each digit contains P bits, The
largest any single digit can be is 2P-1. Each term in a convolution product can be no
greater than (2P-1)2, and there are at most N/P terms
contributing to a single convolution product.
This implies that
(2P-1)2(N/P) <= 2B (I)
as shown below:
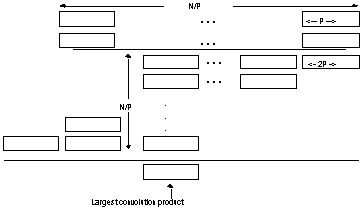
Figure 1: Convolution Products of N/P P-bit digits
Taking the log of both sides, we have
2 log (2P-1) + n - p <= B (II)
It would be convenient to approximate log(2P-1)
by P. Letting e = P - log(2P-1), we have
2(P-e) + n - p <= B (III)
or equivalently
2P + n - p <= B + 2e (IV)
For
P = 1 or a power of two > 2, e is positive and we
may thus neglect it in IV. If P=2, e is approximately -.58.
Neglecting e will give the relation n <= B - 3, while including
it gives n <= B-4.16. Taking n = B-3,
the largest value that satisfies the approximate inequality but not the true
one, we plug P=2 and N = 2n = 2B-3 back into (I) to
obtain
9(2B-4) <= 2B (for P=2, N=2B-3) (V)
This
inequality simplifies to 9 <= 16.
Therefore we may neglect e in (IV) for the
case of P=2 as well. This gives:
2P + n - p <= B (VI)
Suppose we now employ a d-dimensional FNT to compute
the convolution of the input sequences, d > 1. We continue the analysis presented in
[2]. Although only 2-dimensional transforms
are discussed, the process of extension to higher dimensions is
straightforward. Employing a
d-dimensional transform extends a 1-dimensional array into a d-dimensional
hypercube, doubling the length along d-1 axes.
Thus a sequence of length L digits is transformed into a d-dimensional
cube of 2d-1*L elements. For
convenience, we assume L is a power of 2.
The lengths of each axis are distributed as evenly as possible, again as
powers of 2. To perform a 4-dimensional
FNT on a sequence of 210 elements, for example, would require a
total of 23*210 = 213 processors, arranged in
a 24 x 23 x 23
x 23 4-cube.
Let n-p, the logarithm of the sequence length in
digits, be congruent to r mod d. We
distinguish 3 cases: r = 0, r = 1, and r >= 2. If r = 0, there will be d-1 long axes with
log length equal to Î (n-p)/d _+1, and one short
axis of length (n-p)/d. If r = 1, all
axes are of log length Î
(n-p)/d _ + 1; in this
case we say the transform is balanced. If r >= 2, d-1 axes must have their
lengths doubled, but d-r of them can be doubled without increasing the longest
axis length. Any axes remaining must
have their lengths doubled. Thus
d-1-(d-r) = r-1 long axes will have log length Î(n-p)/d_+2, and d-r+1 axes will have log length Î(n-p)/d_+1.
For
example, suppose that n-p = 10, corresponding to a sequence of 1K digits, and
that d=4. Then r = n-p mod d = 2. We can split 210 into 23
x 23 x 22 x 22. Three axis lengths will be doubled by the
transformation, giving 24 x 23 x 23 x 23. We see that r-1 = 1 axis has log length = Î(n-p)/d_+2 = 4, and that d-r+1 = 3 axes have log length = Î(n-p)/d_+1 = 3. If
instead n-p=8, we split 28 into 22 x 22 x 22
x 22, and double three axis lengths to obtain 23 x 23
x 23 x 22. r=0,
and we see that d-1 = 3 axes have log length 8/4 + 1 = 3, and that one axis has
log length 2.
A
multidimensional FNT is similar to other multidimensional transforms; it is
computed by computing 1-dimensional transforms along each dimension. Thus B must be large enough for an FNT of
length 4B to cover any side of the cube.
Depending on the congruence class of n-p mod d, we have either
4B = 2 ( Î(n-p)/d_+2)
(n-p mod d >= 2) (VII)
or
4B =
2
( Î(n-p)/d_+1) (n-p mod d _
0, 1) (VIII)
Using logarithmic notation, these become
b = Î(n-p)/d_ (n-p
mod d >= 2 ) (IX)
and
b = Î(n-p)/d_ -1 (n-p mod d _
0, 1) (X)
Equations
VI, IX, and X give us the defining relationships between n,p,d, and b. For a
given N and d, we may examine the various tradeoffs involved in digit size,
interprocessor communication, and the number of processors required.
Tradeoffs in the FNT
For
any input sequence of N bits, there are a variety of choices regarding its
partitioning into digits, the dimensionality of the transform, the number of
processing elements required, and the number of interprocessor communication
steps.
We
see that the log of the total number of processors required for a d-dimensional
FNT is d -1 + n-p, where n = log N and p is the log of the digit size. We also note that the number of communication
steps required, assuming sufficient processors are available, is equal to the
sum of the logarithms of the lengths of each dimension of the d-cube. For balanced transforms, we substitute (X)
into (VI) to obtain
2p+1+n-p
<= 2 (Î(n-p)/d_ -1 (n-p _ 1 mod d) (XI)
For unbalanced transforms, we may try differing values
of p, using (XI) if n-p _ 0 mod d, or (XII) if n-p mod d >= 2:
2p+1+n p
<= 2 (Î(n-p)/d_) (n-p >= 2 mod d) (XII)
(XI) and (XII)
have no closed form solution for p as a function of n and d. However, for n sufficiently large, we may
neglect the linear terms if we subtract 1 from the exponent on the left hand
side. Thus (XI) simplifies to
p+1 <= (Î(n-p)/d_) - 2 (XIII)
for n sufficiently large, using balanced transforms.
Since
n-p _ 1 mod d, Î(n-p)/d_ = (n-p-1)/d. Multiplying both
sides by d and solving for p gives
p <= (n-3d -1)/(d+1) (n-p _ 1 mod d) (XIV)
Since
p must be an integer, we have
p <= Î(n-3d-1)/(d+1)_ (n-p _ 1 mod d) (XV)
(XV)
applies only for n sufficiently large.
(XI) may be used for any n by an examination of all feasible values of
p. This value of p can then be used in
(X) to compute the smallest b for which the appropriate FNT exists. A graph of the minimum value of b for
balanced transforms, 1 <= n <= 30, 1 <= d <= 4, is shown below.
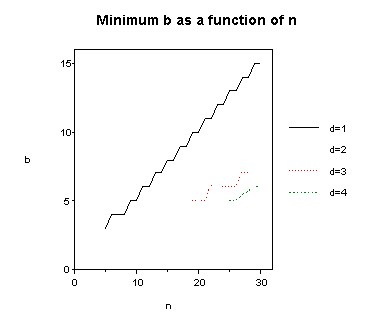
Figure 1
We
have seen that the log of the number of processing elements required is
n-p+d-1. Combining this with (X) shows
that the log number of PEs is d(b+2), making the number of PEs 2d(b+2). The computation of a 1-d FNT along an axis of
the d-cube (using a transform based on a = 4B) requires b+2
interprocessor communication steps. Thus
if n-p _ 1 mod d, the total number of communication steps
required for a d-dimensional FNT is d(b+2), and for convolution 2d(b+2). We note that this is just 2 times the log of the number of PEs.
(Convolution
actually requires the computation of three transforms: two forward and one
inverse. We combine the interprocessor
communication operations of the two forward transforms, transmitting two data
values at once. Thus the communication
operations of the forward transform may take slightly longer than those of the
inverse transform, depending on the values of b and the overhead associated
with interprocessor communication).
We
see that the geometric decrease in word size caused by increasing d is
accompanied by an exponential growth in the number of PE's, and linear growth
in the number of communication steps.
This is shown below in Figures 2 and 3.

Figure 2

Figure 3
Due to the dramatic increase in the number of PEs with
increasing d, it may be desirable to trade off word size for processing
elements. This can be done by using
primitive roots of unity <> 2(1/2), or by using unbalanced
transforms. This is discussed in more
detail in [5].
An Implementation on a Massively Parallel
Processor
The
FNT and other number-theoretic transforms can be used for any application in
which convolution is required. They are
particularly well suited for the computation of exact convolution, and hence
are useful for the multiplication of large integers. We have implemented a program to multiply
large integers on the Connection Machine, using the parallel FNT.
The
Connection Machine is a massively parallel SIMD processor, with processing
elements interconnected in a boolean n-cube.
CM software provides support for "virtual processors",
permitting programs to be written for a number of PEs greater than those
physically available. When the number of
virtual processors exceeds the number of physical processors, the system is
said to be saturated. Further increases
in the number of virtual processors result in a corresponding decrease in
execution time, although this can be affected by interprocessor communication
patterns. For more information on the
Connection Machine, the reader is referred to [7] and [8].
Figure
4 shows a log/log plot of multiplication time as a function of input size,
shown numerically in Table I. We have
implemented a 2D FNT-based algorithm, using balanced transforms with a=2. The values of b mandated by
a 1-D transform would make the point-by-point multiplication performance
unacceptable, while transforms with d > 2 would saturate the system with
processing elements. The results shown
are for a 32K Connection Machine. Values
of n corresponding to n-p+1 > 15, in
this case n >= 17, would execute in approximately half the time on a 64K
CM. (The +1 is due to zero padding of
the input sequences). Execution times
range from 49 milliseconds for 2Kbit numbers to 2600 milliseconds for 8Mbit
numbers.
We
see that the execution time is a very jagged function of n. This is because the dominant factor in
execution time is the number of digits, not the input size in bits. Since a doubling of the input size does not
necessarily result in any increase in the number of digits, resulting in
similar execution times. Implementing
unbalanced transforms would permit the optimal value of p to be used, resulting
in a smoother function.
The
largest numbers our program can multiply are 8Mbits wide. Larger numbers exceed the memory limitations of
a 32K CM, due to the number of processing elements required.
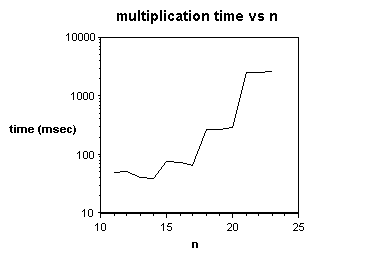
Figure 4
Table I
Multiplication
Time For 2n-bit Integers
n time
(msec)
11 49
12 50
13 40
14 38
15 76
16 72
17 65
18 275
19 275
20 287
21 2500
22 2500
23 2600
We
have reported in previous work [4] our implementation of another integer
convolution algorithm on the Connection Machine. The results reported here
represent an improvement of 6 times for 2K numbers, decreasing to about 4 times
for 8M numbers. The decrease in
performance improvement is due to system saturation, which dampens the
performance effects of otherwise more efficient algorithms.
Conclusions
The
Fermat Number Transform was proposed several years ago as an alternative to the
FFT, but not pursued extensively due to transform length restrictions. For transforms in a Fermat ring modulo 2B+1,
the longest transform length is 4B.
Since b = log B is limited by the word length of the machine computing
the transform, existing computers were limited to short sequences. Multidimensional techniques were proposed to
overcome this restriction, and were partially successful.
The
existence of computers like the Connection Machine, however, make such
restrictions obsolete. The CM does not
make use of the concept of "word length"; operations can be performed
on bit quantities of virtually arbitrary size.
The CM is particularly attractive for the FNT due to the parallel nature
of the algorithm.
Our
results show that while word length restrictions no longer limit the length of
sequences to be used as inputs to the FNT, the parameter b = log B remains
important. The FNT convolution algorithm
requires the point-by-point multiplication of B-bit numbers; if b becomes too
large, point-by-point multiplication time will dominate. For small b, the number of processors and the
number of interprocessor communication steps become the principal factors
affecting performance.
We
have implemented an algorithm for the multiplication of large integers using
the parallel FNT on the Connection Machine.
Our times range from about 50 msec for 2K-bit numbers to 2600 msec for
8Mbit numbers. These results are about 5
times faster than our previous work, an implementation of another integer
convolution algorithm on the Connection Machine [4].
Future
work should focus on reducing interprocessor communication requirements,
perhaps through the use of alternative CM configurations or lower-level CM
instructions than those currently employed by our program. Point-by-point multiplication time could also
be improved through the application of any of the well-known efficient
algorithms for integer multiplication.
Extended-precision FFTs for the CM could also be developed and compared
with the parallel FNT to determine which algorithm is more suitable for large
integer multiplication. Comparisons with
other high-performance architectures would also be useful. Presently, we are combining the program
discussed here with previous work [3] to develop a massively parallel software
library for the arithmetic manipulation of large integers.
Acknowledgements
The
author gratefully acknowledges the use of the Connection Machine Network Server
Pilot Facility, supported under terms of DARPA contract DACA76-88-C-0012 and
made available to the author by Thinking Machines Corporation. Thanks are due in particular to TMC employees
Roger Frye, David Gingold, and Alan Mainwaring
for their patience and assistance.
References
[1] Agarwal, R.C. and Burrus, C.S. "Fast
Convolution Using Fermat Number Transforms With Applications to Digital
Filtering", IEEE Transactions on Acoustics, Speech, and Signal Processing,
vol ASSP-22 no 2 pp 87-97 Apr 1974.
[2] Agarwal, R.C. and Burrus, C.S. "Fast
One-dimensional Digital Convolution by Multidimensional Techniques", IEEE
Transactions on Acoustics, Speech, and Signal Processing, vol ASSP-22 pp 1-10
Feb 1974.
[3] Fagin, Barry,
"Fast Addition of Large Integers", submitted to IEEE
Transactions on Computers, 1989. (Copies
available from the author).
[4] Fagin, Barry, "Negacyclic Convolution Using
Polynomial Transforms on Hypercubes", submitted to IEEE Transactions on
Acoustics, Speech and Signal Processing.
(Copies available from the author).
[5] Fagin, Barry, "Large Integer Multiplication
on Massively Parallel Processors", submitted to the Journal of Parallel
and Distributed Computing, 1990 (Copies available from the author).
[6] Leibowitz, L.M. "A Simplified Binary
Arithmetic for the Fermat Number Transform", IEEE Transactions on
Acoustics, Speech, and Signal Processing, vol. ASSP-24, pp 356-359, October
1976.
[7] Thinking Machines Corporation, Connection Machine Technical Summary,
Cambridge Massachusetts,1989.
[8] Thinking Machines Corporation, C/Paris 5.1 User's
Manual, Cambridge Massachusetts, 1988.